CF-Educational-25 E-Minimal Labels (拓扑排序）

发表于 |
字数统计: 694字 | 阅读时长 ≈ 4min

You are given a directed acyclic graph with n vertices and m edges. There are no self-loops or multiple edges between any pair of vertices. Graph can be disconnected.

You should assign labels to all vertices in such a way that:

  • Labels form a valid permutation of length n — an integer sequence such that each integer from 1 to n appears exactly once in it.
  • If there exists an edge from vertex v to vertex u then labelv should be smaller than labelu.
  • Permutation should be lexicographically smallest among all suitable.

Find such sequence of labels to satisfy all the conditions.

Input

The first line contains two integer numbers n, m (2 ≤ n ≤ 105, 1 ≤ m ≤ 105).

Next m lines contain two integer numbers v and u (1 ≤ v, u ≤ n, v ≠ u) — edges of the graph. Edges are directed, graph doesn’t contain loops or multiple edges.

Output

Print n numbers — lexicographically smallest correct permutation of labels of vertices.

Examples

input

1
2
3
4
3 3
1 2
1 3
3 2

output

1
1 3 2

input

1
2
3
4
5
6
4 5
3 1
4 1
2 3
3 4
2 4

output

1
4 1 2 3

input

1
2
3
4
5
5 4
3 1
2 1
2 3
4 5

output

1
3 1 2 4 5

此题是拓扑排序裸题，但字典序要注意。取出节点时要先取出编号大的节点打上编号大的标签（反图），如果直接从小到大找入度为零的点然后编号的话会有反例

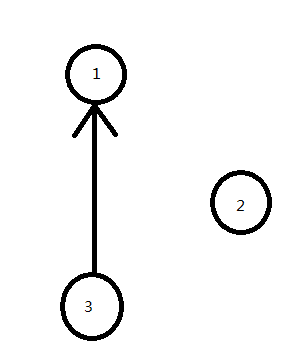
Codeforces-Educational-25-E

如图，如果从小到大讨论的话答案是 3 1 2 但显然正解是 2 3 1

附我naive的wa代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
#include<cstdio>
#include<iostream>
#include<queue>
#include<algorithm>
#define N 2222222
using namespace std;
int n,m,d[N],tot,ans[N];
int TOT,EN[N],NE[N],LA[N];
void ADD(int x,int y)
{
	TOT++;
	EN[TOT]=y;
	NE[TOT]=LA[x];
	LA[x]=TOT;
}
priority_queue<int,vector<int>,greater<int> >q;
int main()
{
	int i,j,x,y;
	cin>>n>>m;
	for(i=1;i<=m;i++)
	{
		scanf("%d%d",&x,&y);
		d[y]++;ADD(x,y);
	}
	for(i=1;i<=n;i++)if(d[i]==0)q.push(i);
	while(!q.empty())
	{
		x=q.top();
		q.pop();
		ans[x]=++tot;
		for(i=LA[x];i;i=NE[i])
		{
			y=EN[i];
			if(d[y]>0)
			{
				d[y]--;
			    if(d[y]==0)q.push(y);
			}
		}
		
	}
	for(i=1;i<=n;i++)printf("%d ",ans[i]);
}

附ac代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
#include<cstdio>
#include<iostream>
#include<queue>
#include<algorithm>
#define N 222222
using namespace std;
int n,m,d[N],tot,ans[N];
int TOT,EN[N],NE[N],LA[N];
void ADD(int x,int y)
{
	TOT++;
	EN[TOT]=y;
	NE[TOT]=LA[x];
	LA[x]=TOT;
}
priority_queue<int>q;
int main()
{
	int i,j,x,y;
	cin>>n>>m;
	for(i=1;i<=m;i++)
	{
		scanf("%d%d",&x,&y);
		d[x]++;ADD(y,x);
	}
	for(i=1;i<=n;i++)if(d[i]==0)q.push(i);
	tot=n;
	while(!q.empty())
	{
		x=q.top();
		q.pop();
		ans[x]=tot--;
		for(i=LA[x];i;i=NE[i])
		{
			y=EN[i];
			if(d[y]>0)
			{
				d[y]--;
			    if(d[y]==0)q.push(y);
			}
		}
		
	}
	for(i=1;i<=n;i++)printf("%d ",ans[i]);
}