选数
问题描述
我们知道,从区间[L,H](L和H为整数)中选取N个整数,总共有(H-L+1)N种方案。小z很好奇这样选出的数的最大公约数的规律,他决定对每种方案选出的N个整数都求一次最大公约数,以便进一步研究。然而他很快发现工作量太大了,于是向你寻求帮助。
你的任务很简单,小z会告诉你一个整数K,你需要回答他最大公约数刚好为K的选取方案有多少个。由于方案数较大,你只需要输出其除以1000000007的余数即可。
输入格式
输入一行,包含4个空格分开的正整数,依次为N,K,L和H。
输出格式
输出一个整数,为所求方案数。
样例输入
2 2 2 4
样例输出
3
提示
样例解释:
所有可能的选择方案:(2,2), (2,3), (2,4), (3,2), (3,3), (3,4), (4,2), (4,3), (4,4)。
其中最大公约数等于2的只有3组:(2,2), (2,4), (4,2)。
数据范围:
对于30%的数据,N≤5,H-L≤5。
对于100%的数据,1≤N,K≤10^9,1≤L≤H≤10^9,H-L≤10^5。
首先,在[L,H]中选最大公约数为K的N个数显然等价于[L/K,H/K]中选最大公约数为1的N个数。
因此,令A=(L-1)/K,B=H/K
(为何要-1呢,主要是因为后面要用减法求可行数的范围(类似于前缀和)而除K后是要取整的,所以范围在这里先确定下来)
推导一下:
这样,如果我们能求出u的前缀和,那么就可以在$\sqrt{n}*\log{n}$的复杂度内解决这个问题。
但是,当H很大而K很小时,B可能会很大以至于线性筛无法解决,这个时候我们可以用传说中的杜教筛来解决。他的数学基础是: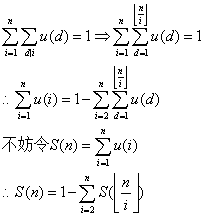
这样,我们就可以递归的求出我们想要的前缀和了,注意到当n比较小的时候我们是可以线性筛求出来的。所以设置一个分界U,当n<=U时用线性筛预处理。并且,经过复杂的推导我们知道当U=$n^{\frac{2}{3}}$最小为$n^{\frac{2}{3}}$
具体实现可以参考代码1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
using namespace std;
map<ll,ll>Q;
ll p[U+5],mu[U+5],smu[U+5],tot,mod=1000000007;
bool mark[U+5];
ll QM(ll a,ll b)
{
ll ans=1;a%=mod;
while(b)
{
if(b&1)ans=ans*a%mod;
b>>=1;
a=a*a%mod;
}
return ans;
}
void EU()
{
mu[1]=1;smu[1]=1;
for(ll i=2;i<=U;i++)
{
if(!mark[i])p[++tot]=i,mu[i]=-1;
for(ll j=1;j<=tot&&p[j]*i<=U;j++)
if(i%p[j])mark[i*p[j]]=1,mu[i*p[j]]=-mu[i];
else {mark[i*p[j]]=1;mu[i*p[j]]=0;break;}
smu[i]=(smu[i-1]+mu[i])%mod;
}
}
ll Mu(ll n)
{
if(n<=U)return smu[n];
if(Q.count(n))return Q[n];
ll ans=1,j,i;
for(i=2;i<=n;i=j+1)
{
j=n/(n/i);
ans=(ans-Mu(n/i)*(j-i+1)%mod)%mod;
}
Q[n]=ans;
return ans;
}
int main()
{
ll N,K,L,H,i,j,ans=0;
scanf("%lld%lld%lld%lld",&N,&K,&L,&H);
EU();L=(L-1)/K;H=H/K;
for(i=1;i<=H;i=j+1)
{
j=H/(H/i);
if(L/i)j=min(j,L/(L/i));
ans=(ans+(Mu(j)-Mu(i-1))*QM(H/i-L/i,N)%mod)%mod;
}
cout<<(ans+mod)%mod;
}