NKOJ3958 （CQOI 2015）JZPTAB（莫比乌斯反演）

发表于 |
字数统计: 428字 | 阅读时长 ≈ 2min

问题描述

NKOJ3958-1

输入格式

一个正整数T表示数据组数。

接下来T行 每行两个正整数 表示N、M。（T <= 10000；N, M<=10000000）

输出格式

共T行，每行一个整数 表示第i组数据的结果。

样例输入 1

1
4 5

样例输出 1

122

样例输入 2

5
555 785
450 317
28 26
284 132
602 341

样例输出 2

64864969
41243780
103158
59672364
39607508

话不多说，直接推导

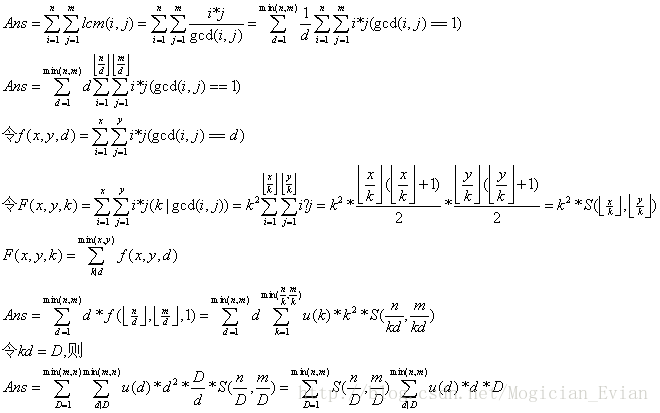
NKOJ3958-2

S可以O(1)求出来，后面的一坨显然是积性的，只需要将后面的求和在线性筛的时候预处理出来即可。
线性筛部分具体可参见代码。于是就可以在根号的复杂度内完成每次询问。最后注意要多取模，尤其是在算S的时候。(亲测30分)

附上代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
#include<stdio.h>
#include<iostream>
#include<algorithm>
#include<cstring>
#define ll long long
#define N 10000005
using namespace std;
ll T,n,m,p[N],g[N],s[N],ans,tot,mod=100000009;
bool mark[N];
int main()
{
	ll t,q,i,j;
	scanf("%lld",&T);
	g[1]=1;s[1]=1;
	for(i=2;i<N;i++)
	{
		if(!mark[i])p[++tot]=i,g[i]=(i-i*i)%mod;
		for(j=1;j<=tot&&i*p[j]<N;j++)
		if(i%p[j])mark[i*p[j]]=1,g[i*p[j]]=g[i]*g[p[j]]%mod;
		else {mark[i*p[j]]=1;g[i*p[j]]=g[i]*p[j]%mod;break;}
		s[i]=(s[i-1]+g[i])%mod;
	}
	while(T--)
	{
		scanf("%lld%lld",&n,&m);
		t=min(n,m);ans=0;
		for(i=1;i<=t;i=j+1)
		{
			j=min(n/(n/i),m/(m/i));
			q=(((n/i)*(n/i+1)>>1)%mod)*(((m/i)*(m/i+1)>>1)%mod)%mod;
			ans=(ans+q*(s[j]-s[i-1])%mod)%mod;
		}
		printf("%lld\n",(ans+mod)%mod);
	}
}