NKOJ 3611(CQOI 2016) 不同的最小割（分治+最小割=最小割树）

发表于 |
字数统计: 1,896字 | 阅读时长 ≈ 8min

P3611【CQOI2016 Day1】不同的最小割

问题描述

学过图论的同学都知道最小割的概念：对于一个图，某个对图中节点的划分将图中所有节点分成两部分，如果节点s,t不在同一个部分中，则称这个划分是关于s,t的割。对于带权图来说，将所有顶点处在不同部分的权值相加所得到的定义为这个割的容量，而s,t的最小割指的是在关于s,t的个中容量最小的割。
而对冲刺NOI竞赛的选手而言，求带权图中两点的最小割已经不是什么难事。我们可以把视野放宽，考虑有N个点的无向连通图中所有点对的最小割容量，共能得到N(N-1)/2个数值。这些数值中互不相同的有多少个呢？这似乎是一个有趣的问题。

输入格式
输入格式

输入文件第一行包含两个数N,M，表示点数和边数。
接下来M行，每行三个数u,v,w，表示点u和点v（从1开始标号）之间有条边权值为w。

输出格式

输出文件第一行为一个整数，表示个数。

样例输入

4 4
1 2 3
1 3 6
2 4 5
3 4 4

样例输出

3

提示

数据范围：
​ 对于50%的数据，N≤200，M≤2000；
​ 对于100%的数据，1≤N≤850，1≤M≤8500,1≤w≤100000
​

题意大概就是让任选点对(x,y)求他们的最小割，最后统计这些最小割中不同的有多少个。
一个显然的想法是，我们可以求出所有的最小割然后统计。但是这样就需要$n^2$次SAP，显然要超时。
这种时候，就可以使用分治最小割-最小割树的方法来求解了。

以下内容均针对无向图

首先，不同的最小割数量不超过n-1个（一个割将点的集合分成两个独立的点集，而最多可以分成n个点集）
事实上，这些最小割构成一颗最小割树，构建过程就是每次选在同一个集合中的两点求最小割然后递归的求最小割，比如我们举个栗子

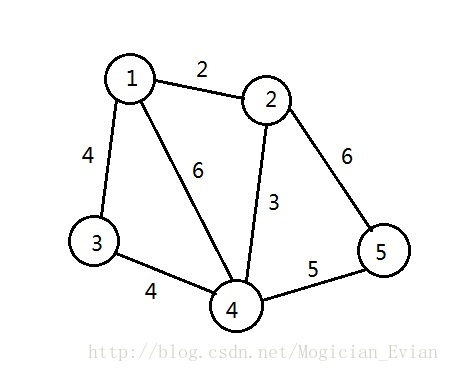
NKOJ3611-1

在这幅图中，我们先任选两个点比如(1,2)来求最小割，肉眼目测应该是10，并且将点集划分为｛1，3，4｝和｛2，5｝两个集合，我们用一条横线来表示这个最小割

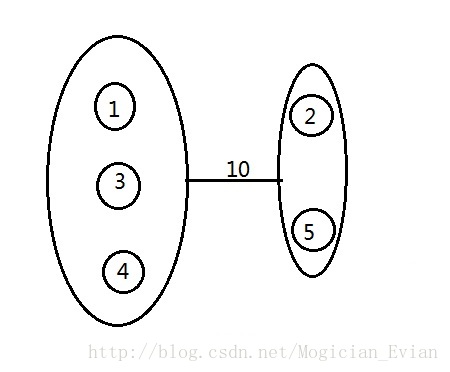
NKOJ3611-1

显然，在两个集合中任取两个点，他们的最小割不超过10。然后我们求(2,5)的最小割，显然是11。
之后求(1,4)的最小割，显然是12，这两次之后，同样用一条边来代表最小割，于是得到

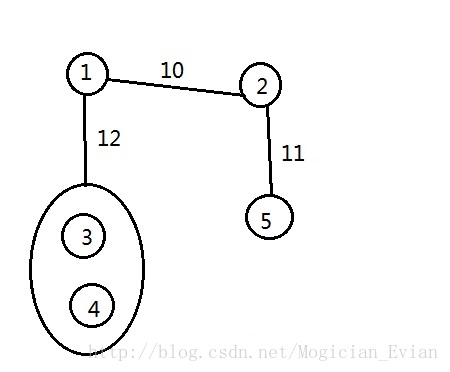
NKOJ3611-1

最后求(3,4)的最小割，得到一颗完整的最小割树

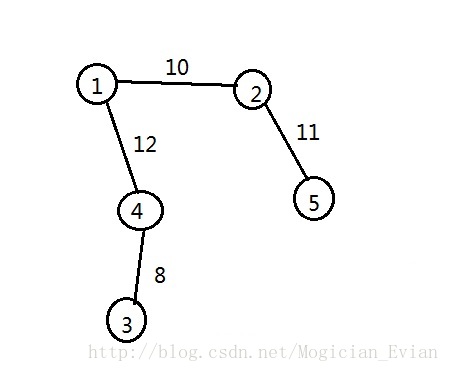
NKOJ3611-1

注意到，以上的点的选择是可以任意选择的，得到这颗树具有一个厉害的性质，即任意两点的最小割等于这棵树上两点间路径经过的边的权值的最小值。注意连边必须是在所求最小割的两点间。

以下提供伪证，可作理解，已经懂了请忽略。

首先我们注意到，当我们求（a，b）的最小割C后，可以将集合划分成两个独立的集合S和T，那么连边的意义显然就是这两个集合中各取一个点x和点y，他们的最小割不会大于C，这是显然的。
那么我们来考虑他们的最小割小于C的情况，根据假设我们可以画一个示意图

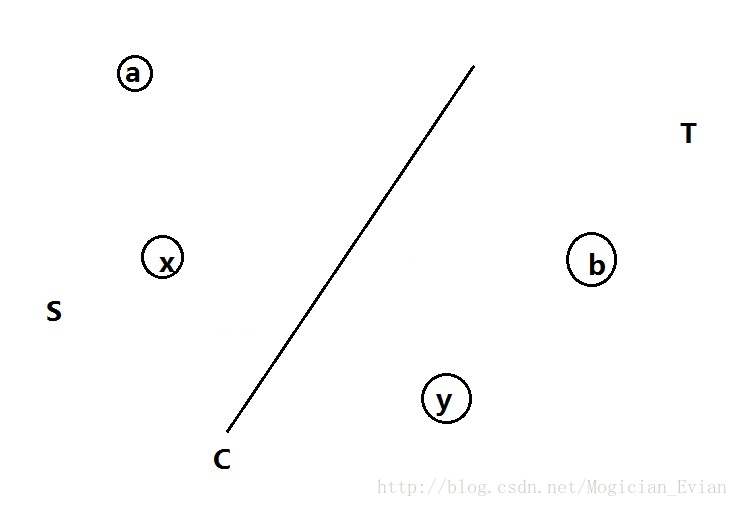
NKOJ3611-1

我们用一条线来代表一个割，两边分别是S集和T集。
如果x，y的最小割D小于C，那么a点和b点必须位于D的同侧，否则C就不是a，b的最小割，同时x，y必须位于D的异侧，那么我们假设x，a，b位于D的同侧

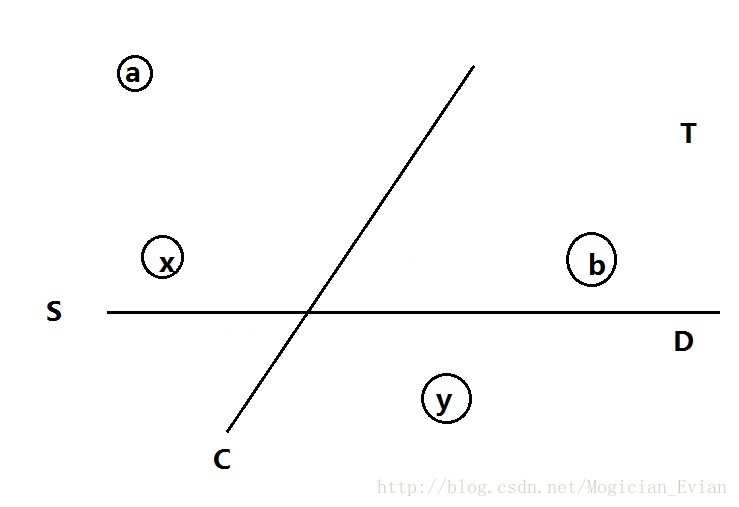
NKOJ3611-1

也就是说，这个割D必然会在我们讨论T集合时被讨论到，他同时是b，y的最小割，因此我们会有y-b的一条边。

因此最后对S和T递归完成后，x，y之间的最小割D一定会被讨论到，因为如果没有被讨论到，说明存在一个较大的割将他们划分入了不同的集合，但显然这是可以递归的证明的。

总结一下，关键就在于如果划分了S集和T集，但存在一个更小的最小割，这个最小割割一定会是S集或T集中的两个点的最小割。

实际代码实现时，我们每次任求一个最小割，然后划分出S集和T集，更新S集和T集之间的最小割，然后递归处理S集和T集。注意的是，假设递归处理了S集，那么更新的时候也必须是对所有点进行更新，而划分却只需要划分S集内部的点。根据上文，在我们递归结束后，所得到的最小割一定不小于实际最小割，同时也不会大于实际的最小割，同时由于最后每个点是一个单独的集合，因此所有点对的最小割一定都被求出来了。
当然，也可以使用连边的方式构造出最小割树。

接着，回到题目，显然就是个模板题了，只需要注意到本题本不需要求出最小割，只需要将每次求出的最小割的值加入一个set中，答案就是set的大小。

附代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
#include<stdio.h>
#include<iostream>
#include<algorithm>
#include<cstring>
#include<set>
#define M 50000
#define H 1234
using namespace std;
int n,m,A[H],B[H],C[H],cntb,cntc;
int TOT=1,LA[M],NE[M],EN[M],G[M],F[M];
int S,T,N,dis[H],cnt[H];
bool vis[H];
set<int>Q;
void ADD(int x,int y,int z)
{
	TOT++;
	EN[TOT]=y;
	G[TOT]=z;
	F[TOT]=z;
	NE[TOT]=LA[x];
	LA[x]=TOT;
}
int SAP(int u,int f)
{
	int i,tmp,d=0;
	if(u==T)return f;
	for(i=LA[u];i>1;i=NE[i])
	if(G[i]&&dis[u]==dis[EN[i]]+1)
	{
		tmp=SAP(EN[i],min(G[i],f-d));
		G[i]-=tmp;
		G[i^1]+=tmp;
		d+=tmp;
		if(d==f||dis[S]>=n)return d;
	}
	if(!--cnt[dis[u]])dis[S]=n;
	cnt[++dis[u]]++;
	return d;
}
void DFS(int x)
{
	int i;
	vis[x]=1;
	for(i=LA[x];i>1;i=NE[i])
	if(G[i]&&(!vis[EN[i]]))DFS(EN[i]);
}
void FZ(int l,int r)
{
	int i,j,flow=0,mid;
	if(l==r)return;
	S=A[l];T=A[r];cntb=cntc=0;
	memset(dis,0,sizeof(dis));
	memset(cnt,0,sizeof(cnt));
	memset(vis,0,sizeof(vis));
	for(i=2;i<=TOT;i++)G[i]=F[i];
	while(dis[S]<n)flow+=SAP(S,1e9);
	Q.insert(flow);
	DFS(S);
	for(i=l;i<=r;i++)
	if(vis[A[i]])B[++cntb]=A[i];
	else C[++cntc]=A[i];
	mid=l+cntb-1;
	for(i=1;i<=cntb;i++)A[l+i-1]=B[i];
	for(i=1;i<=cntc;i++)A[mid+i]=C[i];
	FZ(l,mid);
	FZ(mid+1,r);
}
int main()
{
	int i,j,x,y,z;
	scanf("%d%d",&n,&m);
	for(i=1;i<=m;i++)
	{
		scanf("%d%d%d",&x,&y,&z);
		ADD(x,y,z);ADD(y,x,0);
		ADD(y,x,z);ADD(x,y,0);
	}
	for(i=1;i<=n;i++)A[i]=i;
	FZ(1,n);
	x=Q.size();
	cout<<x;
}