P4040小Q 的表格
问题描述

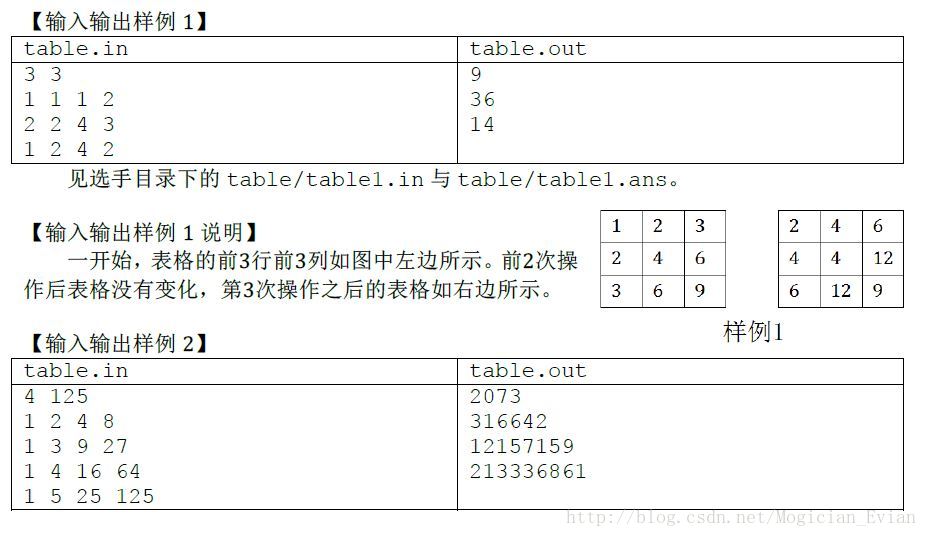

题目给出了一个有规律的表格,因此我们先随便修改一个数找一下所有被修改的数之间有没有什么规律,很容易发现好像被修改的数的行号和列号的gcd是一样的,于是我们考虑证明,实际上我们的修改过程和辗转相减的过程是一样的,因此很容易得证。
接着我们来考虑gcd一样的这些格子的数有什么特点,容易发现他们的倍数关系是固定的,等于行号列号乘积之商,所以我们用 $A[d]$ 表示 $(d,d)$ 这个格子的值,列出求和式
$$Ans=\sum_{d=1}^k A[d] \sum_{i=1}^k \sum_{j=1}^k (gcd(i,j)==d) \frac{ij}{d^2}$$
接下来就有两种做法了。
做法一:
上面的式子看起来很眼熟,于是我们将他变形
$$
Ans=\sum_{d=1}^k A[d] \sum_{i=1}^{\lfloor{\frac{k}{d}}\rfloor} \sum_{j=1}^{\lfloor{\frac{k}{d}}\rfloor}(gcd(i,j)==1) ij
$$
于是莫比乌斯反演一下,
$$
f(x)=\sum_{i=1}^{\lfloor{\frac{k}{d}}\rfloor} \sum_{j=1}^{\lfloor{\frac{k}{d}}\rfloor}(gcd(i,j)==x) ij
$$
$$
F(x)=\sum_{i=1}^{\lfloor{\frac{k}{d}}\rfloor} \sum_{j=1}^{\lfloor{\frac{k}{d}}\rfloor}(x|gcd(i,j)) ij
$$
$$
Ans=\sum_{d=1}^k A[d]\times f(1)=\sum_{d=1}^k A[d] \sum_{x=1}^{\lfloor{\frac{k}{d}}\rfloor} u(x)\times x^2\times [\frac{\lfloor\frac{k}{dx}\rfloor(\lfloor\frac{k}{dx}\rfloor+1)}{2}]^2
$$
现在,我们希望把A[d]后面的一坨解决掉,于是,我们令
$$
g(i)=\sum_{x=1}^{i} u(x)\times x^2\times[\frac{\lfloor\frac{i}{x}\rfloor(\lfloor\frac{i}{x}\rfloor+1)}{2}]^2
$$
$$
Ans=\sum_{d=1}^k A[d]\times g(\lfloor\frac{k}{d}\rfloor)
$$
现在我们发现,如果能预处理出$g(i)$的值,那么可以利用分块的方法在$O(\sqrt{n})$的复杂度内处理每一次询问,问题在于如何预处理,直接算显然不靠谱,我们考虑递推。可以发现,如果$\lfloor\frac{i}{x}\rfloor$和$\lfloor\frac{i-1}{x}\rfloor$是一样的,那么这一项就被减掉了,简单推到一下可以得到
$$
g(i)-g(i-1)=\sum_{x|i} u(x)\frac{i^3}{x}
$$
不妨令右边这一坨为$h(i)$,因此我们有$g(i)-g(i-1)=h(i)$
然后$h(i)$显然是积性的,可以用线性筛搞出来,因此我们可以在$O(n)$的复杂度内搞出我们想要的$g(i)$,之后就可以愉快的分块处理了。
最后还需要注意,分块时我们需要$A[i]$的前缀和,然而用树状数组维护查询是$O(\log{n})$的,肯定要T,
因此我们需要用到分块前缀和这种黑科技,它可以实现$O(\sqrt{n})$插入,$O(1)$查询,方法就是将前缀和数组分块,一般分成$\sqrt{n}$块,然后我们每次更新前缀和相当于将一个区间整体增加一个d,因此我们借鉴线段树的lazy思想,用一个数组记录下整块的更新,然后暴力更新零碎的部分,时间复杂度不超过$O(\sqrt{n})$,查询的时候只需要返回两个数组的和即可。
附上代码
1 |
|
做法二:
做法二非常的厉害,我们先回顾一下做法一中
$$
Ans=\sum_{d=1}^k A[d] \sum_{i=1}^{\lfloor{\frac{k}{d}}\rfloor} \sum_{j=1}^{\lfloor{\frac{k}{d}}\rfloor}(gcd(i,j)==1) ij
$$
然后,厉害的来了,根据欧拉函数的性质,我们有
$$
\sum_{i=1}^{n}i[gcd(i,n)==1]=\frac{n\varphi(n)}{2}
$$
注意到$i$和$j$是相互独立的,于是套用公式,注意到上面公式中$i$是小于$n$的,但是我们要求的式子中,$i$和$j$并没有大小关系,于是需要乘上2,于是我们可以得到
$$
Ans=\sum_{d=1}^{k}A(d)\sum_{i=1}^{\lfloor{\frac{k}{d}}\rfloor}i^{2}\varphi(i)
$$
于是,后面一坨显然是积性的,之后同样分块处理即可。
关于这个公式的证明,注意到如果a和n互质,那么n-a和n也一定互质,因为假设p同时整除n和n-a,那么他一定整除a,矛盾。
以下代码引用自F.F.Chopin,同时不得不说,做法二比做法一跑得要快,因为预处理取模较少,更快。
1 |
|