NKOJ 4042 (CQOI 2017) 老C的方块（最小割+染色）

发表于 |
字数统计: 1,096字 | 阅读时长 ≈ 6min

P4042老C的方块

问题描述
NKOJ4042-1
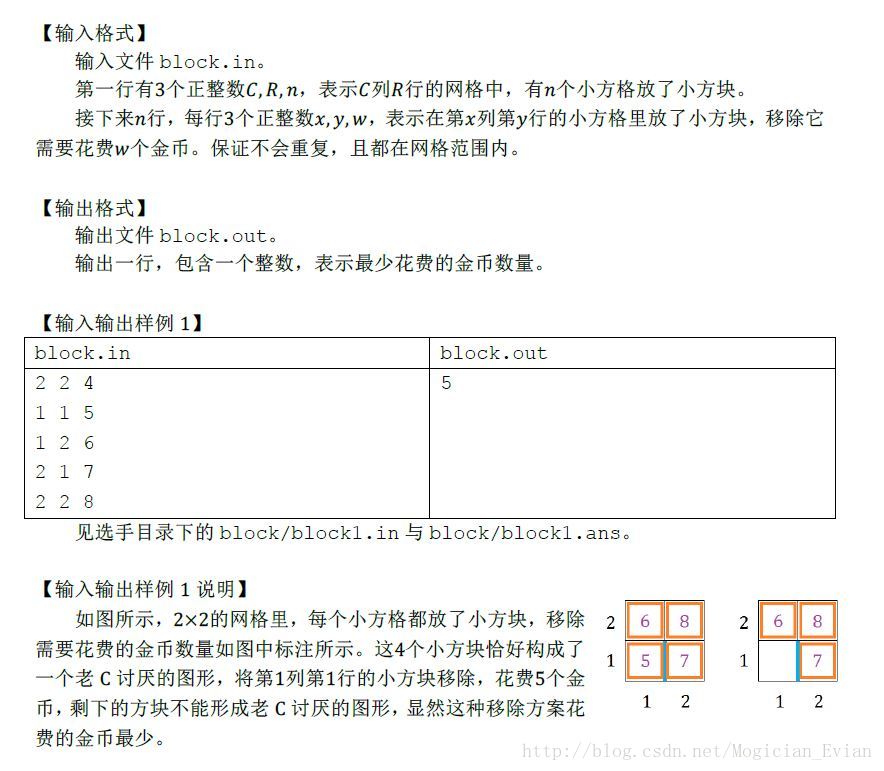
NKOJ4042-2
NKOJ4042-3
NKOJ4042-4

此题比较明显可以想到图论，由于是经典的棋盘问题，我们观察四种讨厌的形状，发现这四种形状有一个共同特点，即都可以看成以特殊边为邻边的两个方块各自再连上一个方块，然后我们发现，特殊边的分布刚好是配合这个规律的，于是我们将棋盘染色

NKOJ4042-5

染色很丑陋，因为是我故意的。
简单说一下，我们将格子分成4类，分别是四种颜色，我们发现，如果一个图形是讨厌的，那么一定满足这个图形是黄-黑-白-蓝，或者黄-白-黑-蓝，于是构图的方法也就出来了
我们新建一个源点S，和一个汇点T。
从S出发连到黄色格子，容量是他的费用。
从黄色格子连到他所相邻的黑色和白色格子，容量无穷大。
相邻黑白格子之间连双向边，容量是黑白格子中费用较小的一个。
从黑白格子出发，连到相邻的蓝色格子，容量无穷大。
从蓝色格子出发，连到汇点T。
最后求出上图的最小割即可。

附上代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
#include<stdio.h>
#include<iostream>
#include<algorithm>
#include<cstring>
#include<map>
#define ll long long
#define N 4234567
using namespace std;
struct node{ll xi,yi,wi,id;};
const ll ct=1000000LL;
ll S,T,C,R,n;
map<ll,node>Q;
node P[N];
ll TOT=1,NE[N],EN[N],G[N],LA[N],dis[N],cnt[N];
void ADD(ll x,ll y,ll z)
{
	TOT++;
	EN[TOT]=y;
	G[TOT]=z;
	NE[TOT]=LA[x];
	LA[x]=TOT;
}
void A1(ll k)
{
	ll t;node tmp;
	ADD(S,k,P[k].wi);ADD(k,S,0);
	t=P[k].xi*ct+ct+P[k].yi;
	if(Q.count(t))
	{
		tmp=Q[t];
		ADD(k,tmp.id,1e18);
		ADD(tmp.id,k,0);
	}
	t-=2*ct;
	if(Q.count(t))
	{
		tmp=Q[t];
		ADD(k,tmp.id,1e18);
		ADD(tmp.id,k,0);
	}
	if(P[k].xi&1)
	{
		t=P[k].xi*ct+P[k].yi+1;
		if(Q.count(t))
		{
			tmp=Q[t];
			ADD(k,tmp.id,1e18);
			ADD(tmp.id,k,0);
		}
	}
	else
	{
		t=P[k].xi*ct+P[k].yi-1;
		if(Q.count(t))
		{
			tmp=Q[t];
			ADD(k,tmp.id,1e18);
			ADD(tmp.id,k,0);
		}
	}
}
void A2(ll k)
{
	ll t;node tmp;
	t=P[k].xi*ct+P[k].yi+1;
	if(Q.count(t))
	{
		tmp=Q[t];
		ADD(k,tmp.id,min(P[k].wi,tmp.wi));
		ADD(tmp.id,k,0);
		ADD(tmp.id,k,min(P[k].wi,tmp.wi));
		ADD(k,tmp.id,0);
	}
}
void A3(ll k)
{
	ll t;node tmp;
	ADD(k,T,P[k].wi);ADD(T,k,0);
	t=P[k].xi*ct+ct+P[k].yi;
	if(Q.count(t))
	{
		tmp=Q[t];
		ADD(tmp.id,k,1e18);
		ADD(k,tmp.id,0);
	}
	t-=2*ct;
	if(Q.count(t))
	{
		tmp=Q[t];
		ADD(tmp.id,k,1e18);
		ADD(k,tmp.id,0);
	}
	if(!(P[k].xi&1))
	{
		t=P[k].xi*ct+P[k].yi+1;
		if(Q.count(t))
		{
			tmp=Q[t];
			ADD(tmp.id,k,1e18);
			ADD(k,tmp.id,0);
		}
	}
	else
	{
		t=P[k].xi*ct+P[k].yi-1;
		if(Q.count(t))
		{
			tmp=Q[t];
			ADD(tmp.id,k,1e18);
			ADD(k,tmp.id,0);
		}
	}
}
ll tp(ll x,ll y)
{
	ll p=y&3;
	if(x&1)return p+1;
	if(p==0)return 3;
	if(p==1)return 1;
	if(p==2)return 4;
	if(p==3)return 2;
}
void edge()
{
	ll i,t;
	for(i=1;i<=n;i++)
	{
		t=tp(P[i].xi,P[i].yi);
		if(t==1)A1(i);
		if(t==2)A2(i);
		if(t==4)A3(i);
	}
}
ll SAP(ll u,ll f)
{
	ll i,v,d=0,tmp;
	if(u==T)return f;
	for(i=LA[u];i>1;i=NE[i])
	{
		v=EN[i];
		if(G[i]&&dis[u]==dis[v]+1)
		{
			tmp=SAP(v,min(f-d,G[i]));
			G[i]-=tmp;
			G[i^1]+=tmp;
			d+=tmp;
			if(f==d||dis[S]>=n+2)return d;
		}
	}
	if(!--cnt[dis[u]])dis[S]=n+2;
	cnt[++dis[u]]++;
	return d;
}
int main()
{
	ll i,x,y,w,ans=0;node tmp;
	scanf("%lld%lld%lld",&C,&R,&n);
	for(i=1;i<=n;i++)
	{
		scanf("%lld%lld%lld",&y,&x,&w);
		tmp.id=i;tmp.wi=w;
		P[i].xi=x;P[i].yi=y;P[i].wi=w;P[i].id=i;
		Q[x*ct+y]=tmp;
	}
	S=n+1;T=S+1;edge();
	while(dis[S]<n+2)ans+=SAP(S,1e18);
	cout<<ans;
}