NKOJ 4239 追捕游戏（LCA）

发表于 |
字数统计: 990字 | 阅读时长 ≈ 5min

P4239追捕游戏

问题描述

何老板最近在玩一款追铺游戏，游戏虽然简单，何老板仍旧乐此不疲。

游戏地图中有n座城市由n-1条双向道路连接。任意两座城市都可相互到达。一名罪犯从A城市出发沿最短路线逃往B城市。在罪犯出发的同时，何老板控制一名警察从C城市出发去追捕那名罪犯。每条道路都有一定的长度(单位米)。罪犯和警察行走的速度相同，都是1秒钟行走1米。

若罪犯到达B城市时还没有被抓住，何老板就输掉了这局游戏。何老板总共玩了m局游戏，每局游戏开始前，何老板想知道他是否能赢下这局游戏，如果能，警察最少行走多少米才能抓到罪犯？

输入格式

第一行，两个整数n和m

接下来n-1行，每行三个整数X,Y,Z，表示城市X和Y之间有一条长度为Z的道路相连。

接下来m行，每行三个整数A,B,C。

输出格式

m行，每行对应一局游戏的结果。若能抓捕到罪犯。输出一个整数，表示警察最少需要行走的距离。若无法抓到罪犯，输出-1。

样例输入

11 2
1 2 6
1 3 3
1 4 3
3 5 2
3 6 5
4 7 9
6 10 3
5 8 4
5 9 3
8 11 8
11 9 10
2 4 7

样例输出

10
9

提示

【样例解释】

第1局在5号城市抓住罪犯。
第2局在4号城市抓住罪犯。

【数据范围】
对于约40% 的数据：1<=N,M<=2000
对于约100% 的数据：1<=N,M<=100000 1<=道路的长度<=10000

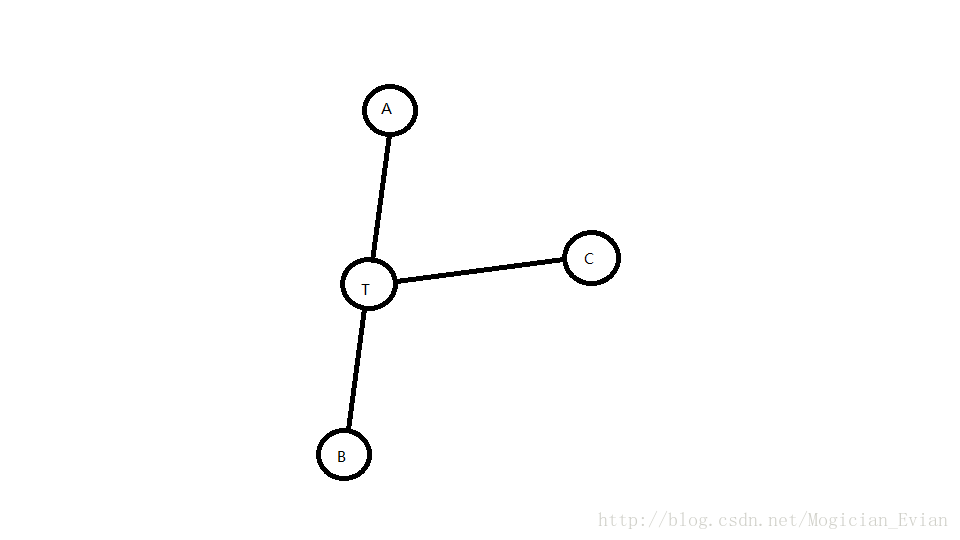
NKOJ4239

此题容易发现A->B的路径是唯一的，因此警察从C到A->B路径上距离C最近的一点T等待是最优的。那么我们需要算出$dis(B,T)$和$dis(C,T)$。
观察可以发现以下关系式。
$$2\times dis(B,T)=dis(A,B)+dis(C,B)-dis(A,C)$$
$$2\times dis(C,T)=dis(A,C)+dis(B,C)-dis(A,B)$$
于是我们就算出了$dis(B,T)$和$dis(C,T)$,然后判断一下谁先到即可。

除此之外，还可以用一个玄学结论，即A,B,C两两求LCA后，必定有两个LCA相同，只出现了一次的那个LCA就是T点。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
#include<stdio.h>
#include<iostream>
#include<algorithm>
#define N 100005
#define M 200005
using namespace std;
int n,m,S=20,fa[N][24],dis[N],dep[N];
int TOT,LA[N],NE[M],EN[M],LE[M];
void ADD(int x,int y,int z)
{
	TOT++;
	EN[TOT]=y;
	LE[TOT]=z;
	NE[TOT]=LA[x];
	LA[x]=TOT;
}
void DFS(int x,int f,int l)
{
	int i,y;
	fa[x][0]=f;
	dis[x]=dis[f]+l;
	dep[x]=dep[f]+1;
	for(i=1;i<=S;i++)fa[x][i]=fa[fa[x][i-1]][i-1];
	for(i=LA[x];i;i=NE[i])
	{
		y=EN[i];
		if(y!=f)DFS(y,x,LE[i]);
	}
}
int LCA(int x,int y)
{
	int i,t;
	if(dep[x]<dep[y])x^=y^=x^=y;
	t=dep[x]-dep[y];
	for(i=0;i<=S;i++)
	if(t&(1<<i))x=fa[x][i];
	if(x==y)return y;
	for(i=S;i>=0;i--)
	if(fa[x][i]!=fa[y][i])x=fa[x][i],y=fa[y][i];
	return fa[x][0];
}
int DIS(int x,int y,int z)
{return dis[x]+dis[y]-2*dis[z];}
int main()
{
	int i,x,y,z,f1,f2,f3,t1,t2;
	scanf("%d%d",&n,&m);
	for(i=1;i<n;i++)
	{
		scanf("%d%d%d",&x,&y,&z);
		ADD(x,y,z);ADD(y,x,z);
	}
	DFS(1,0,0);
	for(i=1;i<=m;i++)
	{
		scanf("%d%d%d",&x,&y,&z);
		f1=LCA(x,y);
		f2=LCA(x,z);
		f3=LCA(y,z);
		t1=DIS(x,y,f1)+DIS(x,z,f2)-DIS(y,z,f3)>>1;
		t2=DIS(x,z,f2)+DIS(y,z,f3)-DIS(x,y,f1)>>1;
		if(t1<t2)printf("-1\n");
		else printf("%d\n",t2);
	}
}