P4241【NOIP2016 DAY2】蚯蚓
问题描述

输入格式
第一行包含六个整数n,m,q,u,v,t,其中:n,m,q的意义见问题描述;
u,v,t均为正整数;你需要自己计算p=u/v(保证0 < u < v)t是输出参数,其含义将会在输出格式中解释。
第二行包含n个非负整数,为ai,a2,…,an,即初始时n只蚯蚓的长度。
同一行中相邻的两个数之间,恰好用一个空格隔开。
输出格式
第一行输出⌊m/t⌋ 个整数,按时间顺序,依次输出第t秒,第2t秒,第3t秒……被切断蚯蚓(在被切断前)的长度。
第二行输出⌊(n+m)/t⌋个整数,输出m秒后蚯蚓的长度;需要按从大到小的顺序
依次输出排名第t,第2t,第3t……的长度。
同一行中相邻的两个数之间,恰好用一个空格隔开。即使某一行没有任何数需要 输出,你也应输出一个空行。
请阅读样例来更好地理解这个格式。
样例输入 1
3 7 1 1 3 1
3 3 2
样例输出 1
3 4 4 4 5 5 6
6 6 6 5 5 4 4 3 2 2
样例输入 2
3 7 1 1 3 2
3 3 2
样例输出 2
4 4 5
6 5 4 3 2
样例输入 3
3 7 1 1 3 9
3 3 2
样例输出 3
2
提示
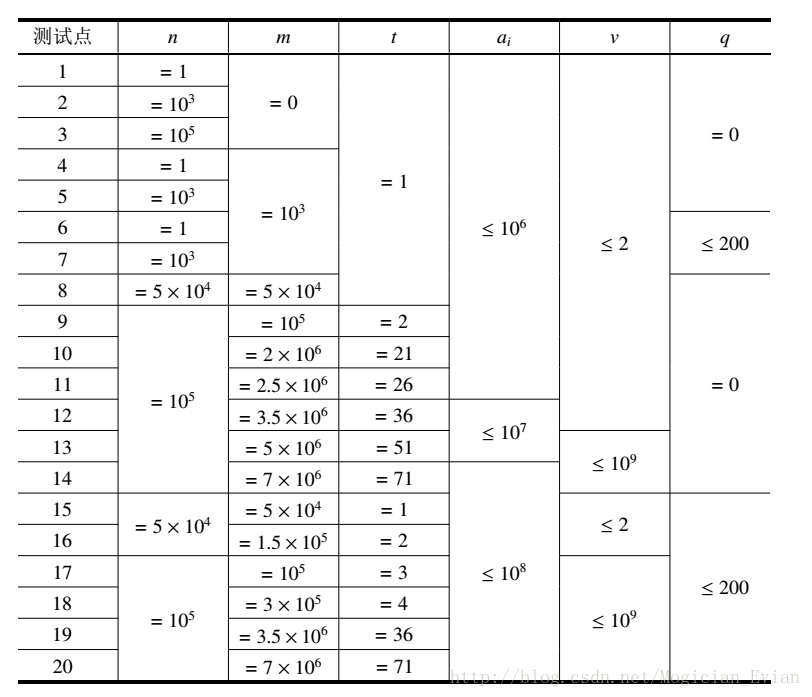
一开始想到用一个堆来维护最长的蚯蚓,用全局标记来解决长度增加。但是这样只能得60分。
鉴于数据范围,我们需要$O(n)$的算法,于是考虑能否维护单调性,我们发现切出的两条蚯蚓中,较大的一条和较小的一条都可以维护单调性,因为如果我们先切长的蚯蚓,那么切出来的较长的蚯蚓肯定比后切的蚯蚓切出的要长,这个证明比较简单。
于是我们可以用三个单调队列来维护,一个队列中存原有的蚯蚓,一个存切出的蚯蚓中较长的一条,一个存切出的蚯蚓中较短的一条,这三个队列都是单调的,因此答案很容易得到。推荐手工队列。
代码:
1 |
|